Como ler binário

Se você estiver interessado em aprender a ler binários, é importante entender como funcionam os números binários. O binário é conhecido como sistema de numeração de “base 2”, o que significa que há dois números possíveis para cada dígito; um um ou zero. Números maiores são escritos adicionando uns ou zeros adicionais ao número binário.

Compreendendo os números binários

Saber ler o binário não é crítico para usar computadores. Mas é bom entender o conceito para obter uma melhor compreensão de como os computadores armazenam números na memória. Ele também permite que você entenda termos como 16 bits, 32 bits, 64 bits e medições de memória como bytes (8 bits).

Como ler o código binário

“Ler” código binário normalmente significa traduzir um número binário em um número de base 10 (decimal) com o qual as pessoas estão familiarizadas. Essa conversão é simples o suficiente de realizar em sua cabeça, uma vez que você entenda como funciona a linguagem binária. B Cada localização de dígito em um número binário tem um valor específico se o dígito não for zero. Depois de determinar todos esses valores, basta adicioná-los para obter o valor de base 10 (decimal) do número binário. Para ver como isso funciona, pegue o número binário 11001010.

1. A melhor maneira de ler um número binário é começar com o dígito mais à direita e seguir para a esquerda. A potência dessa primeira localização é zero, o que significa que o valor desse dígito, se não for zero, é dois elevado a zero, ou um. Nesse caso, como o dígito é zero, o valor dessa casa seria zero.

2. Em seguida, passe para o próximo dígito. Se for um, calcule dois elevado a um. Anote esse valor também. Neste exemplo, o valor é dois elevado a um, que é dois.

   

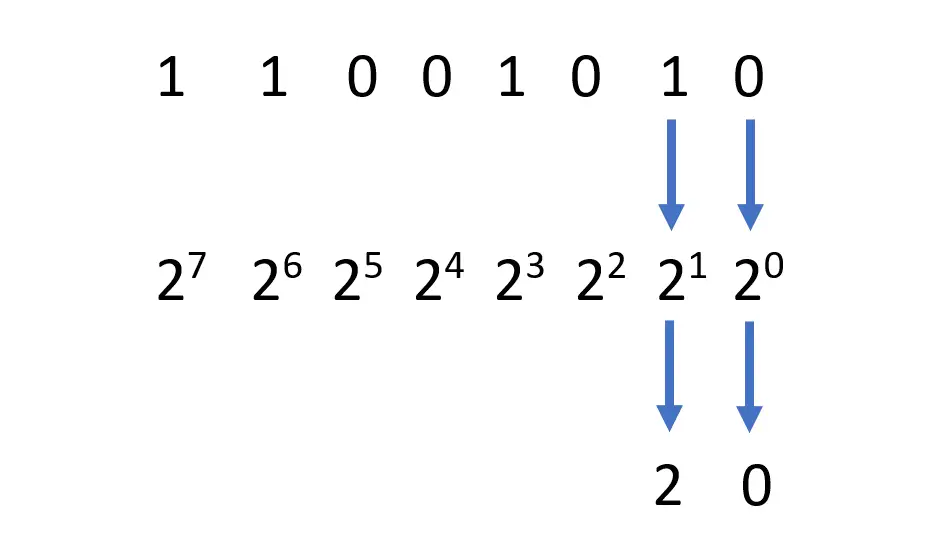
3. Continue a repetir esse processo até chegar ao dígito mais à esquerda.

   

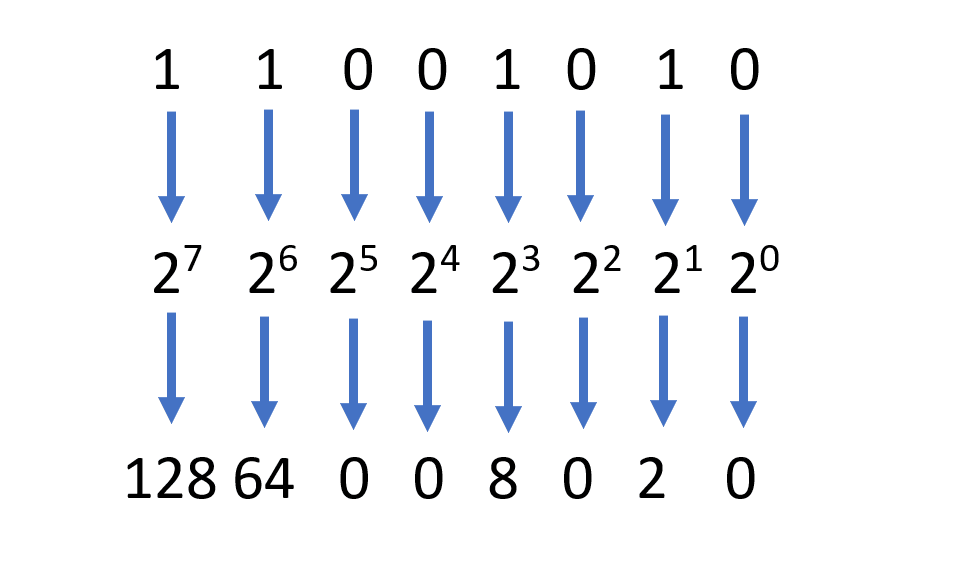
4. Para terminar, tudo o que você precisa fazer é somar todos esses números para obter o valor decimal geral do número binário: 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202

   Outra maneira de ver todo esse processo na forma de equação é a seguinte: 1 x 2⁷ + 1 x 2⁶ + 0 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2⁰ = 202

Números binários assinados

O método acima funciona para números binários sem sinal básicos. No entanto, os computadores precisam de uma maneira de representar números negativos usando binários também. Por causa disso, os computadores usam números binários assinados. Nesse tipo de sistema, o dígito mais à esquerda é conhecido como bit de sinal, enquanto os dígitos restantes são conhecidos como bits de magnitude. Ler um número binário com sinal é quase o mesmo que sem sinal, com uma pequena diferença.

1. Execute o mesmo procedimento descrito acima para um número binário sem sinal, mas pare quando chegar ao bit mais à esquerda.

   

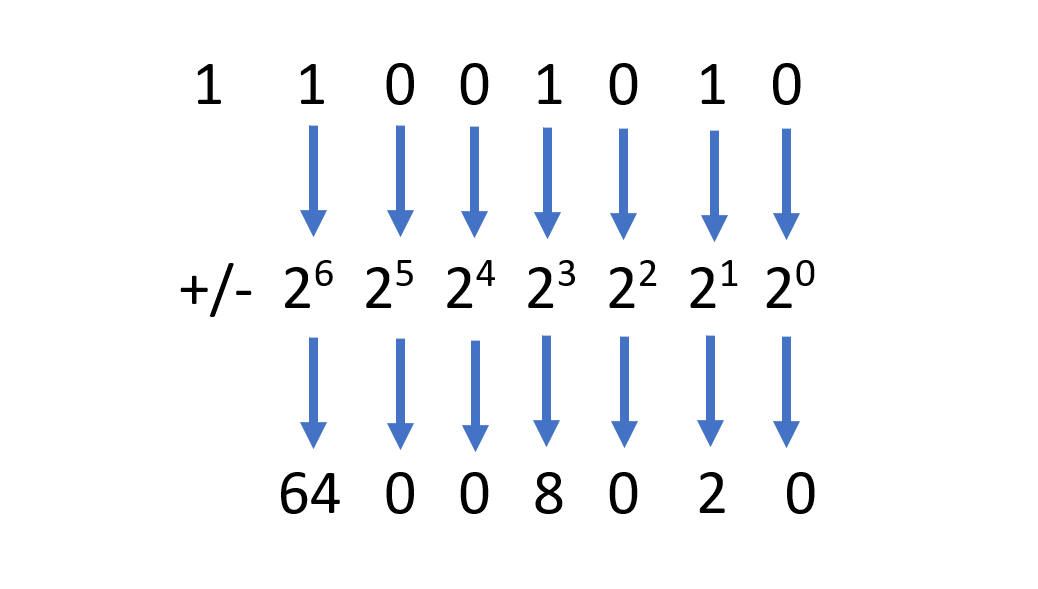
2. Para determinar o sinal, examine o bit mais à esquerda. Se for um, o número é negativo. Se for zero, o número é positivo.

   

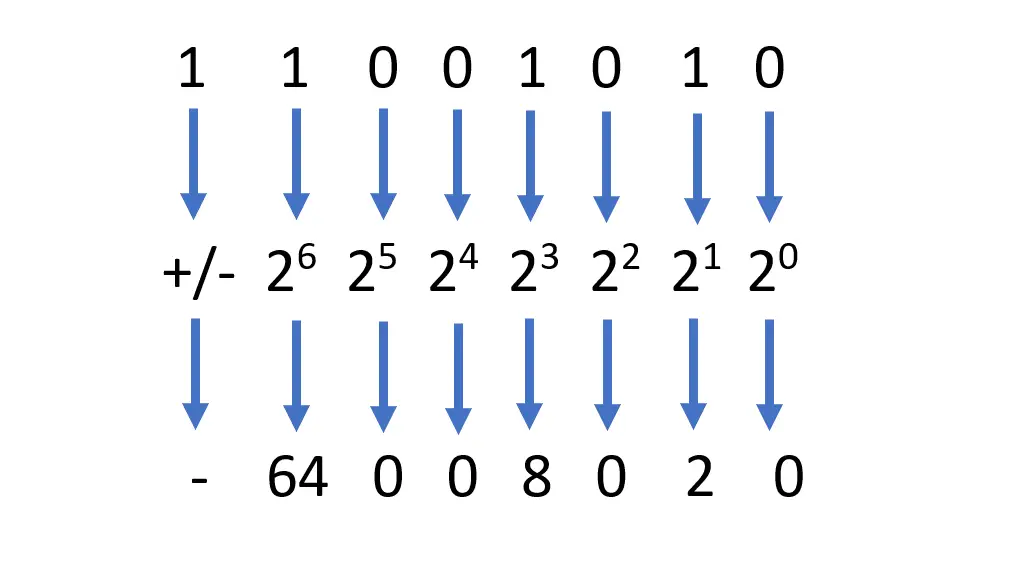
3. Agora, execute o mesmo cálculo de antes, mas aplique o sinal apropriado ao número, conforme indicado pelo bit mais à esquerda: 64 + 0 + 0 + 8 + 0 + 2 + 0 = -74

4. O método binário com sinal permite que os computadores representem números positivos ou negativos. No entanto, ele consome um bit inicial, o que significa que números maiores requerem um pouco mais de memória do que os números binários sem sinal.