Como fazer um teste T no Excel

Neste artigo

Um teste T é uma forma de decidir se existem diferenças estatisticamente significativas entre os conjuntos de dados, usando uma distribuição t de Student. O Teste T no Excel é um teste T de duas amostras que compara as médias de duas amostras. Este artigo explica o que significa significância estatística e mostra como fazer um Teste T no Excel. As instruções neste artigo se aplicam ao Excel 2019, 2016, 2013, 2010, 2007; Excel para Microsoft 365 e Excel Online.

Fonte da imagem, Getty Images

O que é significância estatística?

Imagine que você queira saber qual dos dois dados dará uma pontuação melhor. Você rola o primeiro dado e ganha 2; você rola o segundo dado e obtém um 6. Isso indica que o segundo dado geralmente dá pontuações mais altas? Se você respondeu “Claro que não”, então você já tem algum conhecimento sobre a significância estatística. Você entende que a diferença foi devido à mudança aleatória na pontuação, cada vez que um dado é lançado. Como a amostra era muito pequena (apenas um rolo), ela não mostrou nada significativo. Agora imagine que você rola cada dado 6 vezes:

Os primeiros lançamentos de dados 3, 6, 6, 4, 3, 3; Média = 4,17
O segundo dado rola 5, 6, 2, 5, 2, 4; Média = 4,00

Isso prova que o primeiro dado dá pontuações mais altas do que o segundo? Provavelmente não. Uma pequena amostra com uma diferença relativamente pequena entre as médias torna provável que a diferença ainda seja devida a variações aleatórias. À medida que aumentamos o número de lançamentos de dados, torna-se difícil dar uma resposta de bom senso à pergunta – a diferença entre as pontuações é o resultado de variação aleatória ou é realmente mais provável que um dê pontuações mais altas do que o outro? Significância é a probabilidade de que uma diferença observada entre as amostras seja devido a variações aleatórias. A significância é freqüentemente chamada de nível alfa ou simplesmente ‘α’. O nível de confiança, ou simplesmente ‘c,’ é a probabilidade de que a diferença entre as amostras não seja devida a variação aleatória; em outras palavras, que há uma diferença entre as populações subjacentes. Portanto: c = 1 – α

Podemos definir ‘α’ em qualquer nível que quisermos, para nos sentirmos confiantes de que provamos ser importantes. Muitas vezes α = 5% é usado (95% de confiança), mas se quisermos ter certeza de que quaisquer diferenças não são causadas por variação aleatória, podemos aplicar um nível de confiança mais alto, usando α = 1% ou mesmo α = 0,1 %. Vários testes estatísticos são usados para calcular a significância em diferentes situações. Os testes T são usados para determinar se as médias de duas populações são diferentes e os testes F são usados para determinar se as variâncias são diferentes.

Por que testar a significância estatística?

Ao comparar coisas diferentes, precisamos usar testes de significância para determinar se um é melhor do que o outro. Isso se aplica a muitos campos, por exemplo:

Nos negócios, as pessoas precisam comparar diferentes produtos e métodos de marketing.
Nos esportes, as pessoas precisam comparar diferentes equipamentos, técnicas e competidores.
Na engenharia, as pessoas precisam comparar diferentes projetos e configurações de parâmetros.

Se você quiser testar se algo tem um desempenho melhor do que outra coisa, em qualquer campo, você precisa testar a significância estatística.

O que é a distribuição T de um aluno?

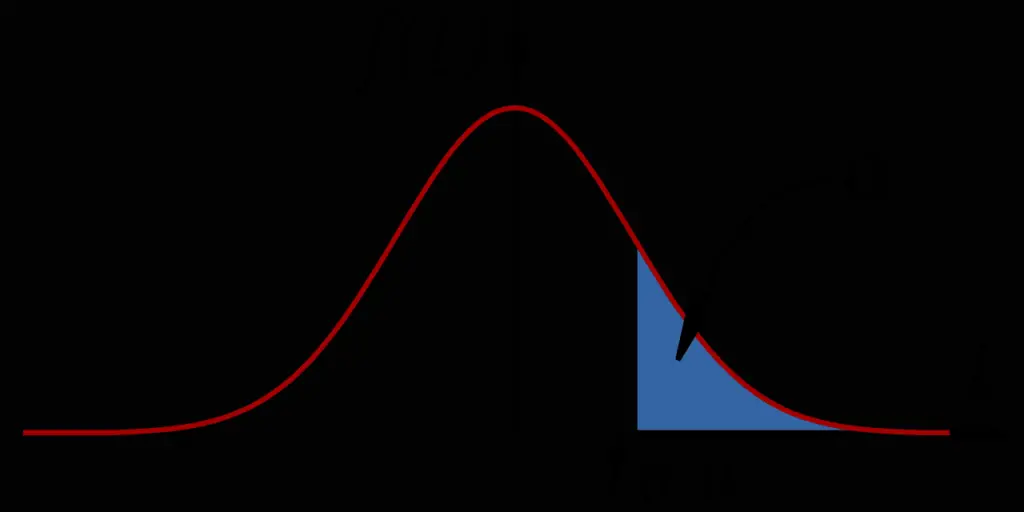
A distribuição t de Student é semelhante a uma distribuição normal (ou gaussiana). Ambas são distribuições em forma de sino com a maioria dos resultados próximos à média, mas alguns eventos raros estão bem longe da média em ambas as direções, chamadas de caudas da distribuição. A forma exata da distribuição t de Student depende do tamanho da amostra. Para amostras de mais de 30, é muito semelhante à distribuição normal. À medida que o tamanho da amostra é reduzido, as caudas ficam maiores, representando o aumento da incerteza que vem de fazer inferências com base em uma pequena amostra.

Como fazer um teste T no Excel

Antes de poder aplicar um Teste-T para determinar se há uma diferença estatisticamente significativa entre as médias de duas amostras, você deve primeiro realizar um Teste-F. Isso ocorre porque cálculos diferentes são executados para o Teste-T, dependendo se há uma diferença significativa entre as variâncias. Você vai precisar do Suplemento Analysis Toolpak habilitado para realizar esta análise.

Verificando e carregando o suplemento Analysis Toolpak

Para verificar e ativar o Analysis Toolpak, siga estas etapas:

Selecione os ARQUIVO guia> selecione Opções.
Na caixa de diálogo Opções, selecione Suplementos nas guias do lado esquerdo.
Na parte inferior da janela, selecione Gerenciar menu suspenso e selecione Suplementos Excel. Selecione Vai.
Certifique-se de que a caixa de seleção ao lado de Analysis Toolpak está marcada, em seguida, selecione OK.
O Analysis Toolpak agora está ativo e você está pronto para aplicar F-Tests e T-Tests.

Executando um Teste F e um Teste T no Excel

Insira dois conjuntos de dados em uma planilha. Nesse caso, estamos considerando a venda de dois produtos durante uma semana. O valor médio das vendas diárias de cada produto também é calculado, juntamente com seu desvio padrão.
Selecione os Dados guia> Análise de dados
Selecione Teste F de duas amostras para variações da lista e, em seguida, selecione OK.

O F-Test é altamente sensível à não normalidade. Portanto, pode ser mais seguro usar um teste de Welch, mas isso é mais difícil no Excel.
Selecione o intervalo da variável 1 e o intervalo da variável 2; definir o alfa (0,05 dá 95% de confiança); selecione uma célula para o canto superior esquerdo da saída, considerando que isso preencherá 3 colunas e 10 linhas. Selecione OK.

Para o intervalo da variável 1, a amostra com o maior desvio padrão (ou variância) deve ser selecionada.
Visualize os resultados do teste F para determinar se há uma diferença significativa entre as variações. Os resultados fornecem três valores importantes:
- F: A proporção entre as variações.
- P (F <= f) unilateral: A probabilidade de que a variável 1 não tenha realmente uma variância maior do que a variável 2. Se for maior que alfa, que geralmente é 0,05, não há diferença significativa entre as variâncias.
- F crítico unicaudal: O valor de F que seria necessário para dar P (F <= f) = α. Se esse valor for maior que F, isso também indica que não há diferença significativa entre as variâncias.
P (F <= f) também pode ser calculado usando a função FDIST com F e os graus de liberdade para cada amostra como suas entradas. Graus de liberdade é simplesmente o número de observações em uma amostra menos um.
Agora que você sabe se há uma diferença entre as variações, você pode selecionar o Teste-T apropriado. Selecione os Dados guia> Análise de dados, em seguida, selecione Teste t: duas amostras assumindo variâncias iguais ou Teste t: duas amostras assumindo variâncias desiguais.
Independentemente de qual opção você escolheu na etapa anterior, será apresentada a mesma caixa de diálogo para inserir os detalhes da análise. Para começar, selecione os intervalos contendo as amostras para Variable 1 Range e Variable 2 Range.
Supondo que você queira testar se não há diferença entre as médias, defina o Diferença média hipotética a zero.
Defina o nível de significância Alfa (0,05 dá 95% de confiança) e selecione uma célula para o canto superior esquerdo da saída, considerando que isso preencherá 3 colunas e 14 linhas. Selecione OK.
Revise os resultados para decidir se há uma diferença significativa entre as médias. Assim como com o teste F, se o valor p, neste caso P (T <= t), for maior que alfa, então não há diferença significativa. No entanto, neste caso, há dois valores de p fornecidos, um para um teste de uma cauda e outro para um teste de duas caudas. Nesse caso, use o valor bicaudal, pois qualquer variável com uma média maior seria uma diferença significativa.